par Sébastien Dumortier
C’est un sujet qui a été traité par Mickaël Launay, grande source d’inspiration pour moi, dans cette vidéo, par Johan Mathieu ici avec de belles illustrations et que l’on retrouve aussi ici (en anglais).
Après une rapide découverte, je vous propose d’explorer un autre aspect de ces jolies tables :
les redondances des représentations.
1. Découverte du concept
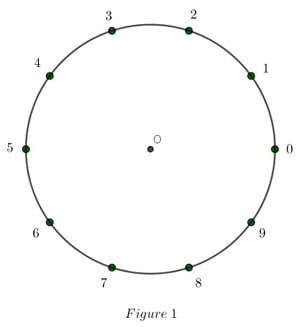
On parcourt ensuite les points \(« 0 »\) à \(« 9 »\) en les reliant, par un segment, à leur double :
\(0×2=0\) donc \(0\) est relié par un segment à lui-même.
\(1×2=2\) donc \(1\) est relié par un segment à \(2\).
\(5×2=10\) et \(10\) correspond à \(0\) modulo \(10\), donc \(5\) est relié à \(0\).
\(6×2=12\) et \(12\) correspond à \(2\) modulo \(10\) , donc \(6\) est relié à \(2\).
\(9×2=18\) donc \(9\) est relié à \(8\) (qui correspond à \(18\))
On représente ainsi la table de multiplication de \(2\), modulo \(10\).
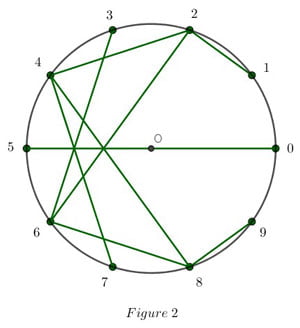
Séquence[Segment[exp(2i*pi*k/10),exp(2i*pi*2k/10)], k, 0, 9]
dans la barre de formule de GeoGebra, on obtient immédiatement la Figure 2.
À ce stade, il est intéressant de créer deux curseurs :
\(m\) entier de \(3\) à \(100\) (exemple) qui représentera le modulo et \(t\) entier de \(0\) à \(m-1\) qui définira la table qu’on souhaite.
Notons que la table de deux entiers égaux modulos \(m\) sera bien sûr la même.
En effet, si \(t_{1}≡t_{2}[m] \) alors pour tout entier \(k\), on aura également \(kt_{1}≡kt_{2}[m]\). Voilà pourquoi on peut se limiter à \([\![0 ;m−1]\!]\) pour \(t\).
Il ne reste plus qu’à adapter la liste de segments, et à jouer.
La fonction séquence est alors modifiée en :
Séquence[Segment[exp(2i*pi*k/m),exp(2i*pi*t*k/m)],k,0,m-1]
On notera que la table du \(1\) ne donne rien, quelle que soit la valeur de \(m\). En fait elle donne des points, puisque tout point est relié à lui-même.
La table du \(0\), elle, donnera toujours le même type de motif, \(0\) étant relié à chacun des points.
2. Identification visuelle des redondances
Voici un petit florilège de jolies tables, avec les valeurs :
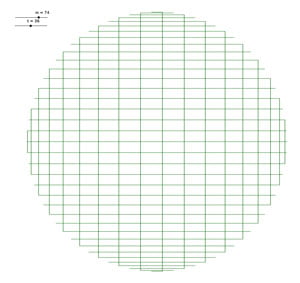
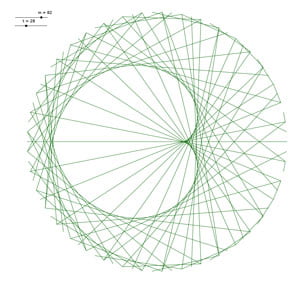
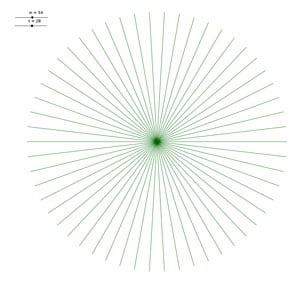
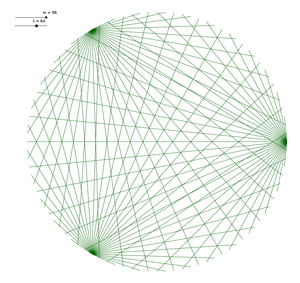
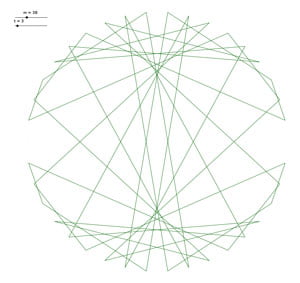
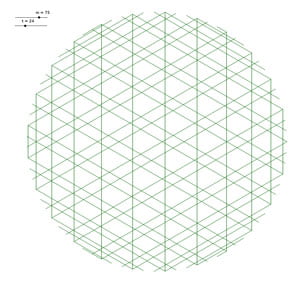
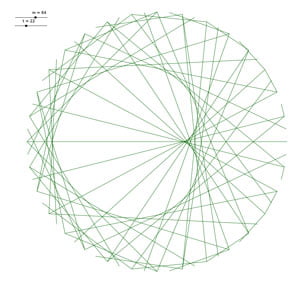
Mais ce ne sont pas \(D\) et \(I\) puisqu’elles n’ont pas le même nombre de points sur le contour.
Il s’agit de \(B\) et \(G\).
A force de jouer avec les images, j’ai voulu connaître le critère qui en rendaient deux identiques.
Il est nécessaire que \(m\) soit le même pour les deux. Je me suis donc appliqué à les passer visuellement une par une en revue, et à lister les doublons.
Pour \(m=3\) et \(m=4\) , il n’y a aucun doublon.
Pour \(m=5\) , les tables de \(2\) et \(3\) donnent les mêmes représentations.
Pas de doublon pour \(6\).
En revanche pour \(m=7\) ça devient intéressant : les tables de \(2\) et de \(4\) sont identiques, ainsi que les tables de \(3\) et de \(5\).
Visuellement, j’ai pu travailler jusqu’à \(m=11\) avant d’éprouver de vraies difficultés à identifier deux motifs, malgré l’aide précieuse de mon épouse, spécialiste du jeu « Le Lynx ».
3. Observation mathématique
La règle empirique qui semblait se dégager était :
si \(a×b≡1[m] \) alors les tables de \(a\) et de \(b\) sont identiques.
Cette règle se confirme :
si \(ka≡λ [m]\) alors \(kab≡λ b [m]\) d’où \(λ b≡k [m]\) ce qui signifie que \(k\) et \(λ\) sont reliés aussi bien
dans la table de multiplication de \(a\) que dans celle de \(b\) , quels que soient \(k\) et \(λ\) .
Ainsi, il est possible de prévoir que les tables de \(6\) et de \(8\) seront identiques modulo \(47\).
En effet, \(6×8=48\) et \(48\) est congru à \(1\) modulo \(47\).
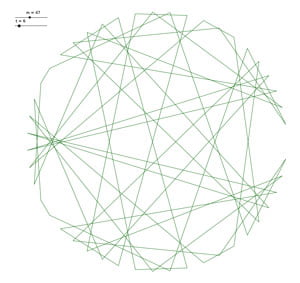
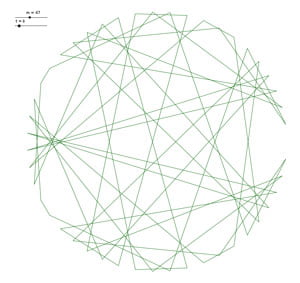
4. Etude de la réciproque
pour \(1 : (0;0) (1;1) (2;2) (3;3) (4;4) (5;5) (6;6)\)
pour \(2 : (0;0) (1;2) (2;4) (3;6) (4;1) (5;3) (6;5)\)
pour \(3 : (0;0) (1;3) (2;6) (3;2) (4;5) (5;1) (6;4)\)
pour \(4 : (0;0) (1;4) (2;1) (3;5) (4;2) (5;6) (6;3)\)
pour \(5 : (0;0) (1;5) (2;3) (3;1) (4;6) (5;4) (6;2)\)
pour \(6 : (0;0) (1;6) (2;5) (3;4) (4;3) (5;2) (6;1)\)
for m in range(3,1001):
seg=[]
for t in range(0,m):
seg.append([])
for k in range(0,m):
seg[t].append([min(k,(t*k)%m),max(k,(t*k)%m)]) Les listes deviennent alors :
pour \(1 : (0;0) (1;1) (2;2) (3;3) (4;4) (5;5) (6;6)\)
pour \(2 : (0;0) (1;2) (1;4) (2;4) (3;5) (3;6) (5;6)\)
pour \(3 : (0;0) (1;3) (1;5) (2;3) (2;6) (4;5) (4;6)\)
pour \(4 : (0;0) (1;2) (1;4) (2;4) (3;5) (3;6) (5;6)\)
pour \(5 : (0;0) (1;3) (1;5) (2;3) (2;6) (4;5) (4;6)\)
pour \(6 : (0;0) (1;6) (1;6) (2;5) (2;5) (3;4) (3;4)\)
for k in range(0,m):
seg[k].sort() Les listes deviennent alors :
pour \(1 : (0;0) (1;1) (2;2) (3;3) (4;4) (5;5) (6;6)\)
pour \(2 : (0;0) (1;2) (2;4) (3;6) (1;4) (3;5) (5;6)\)
pour \(3 : (0;0) (1;3) (2;6) (2;3) (4;5) (1;5) (4;6)\)
pour \(4 : (0;0) (1;4) (1;2) (3;5) (2;4) (5;6) (3;6)\)
pour \(5 : (0;0) (1;5) (2;3) (1;3) (4;6) (4;5) (2;6)\)
pour \(6 : (0;0) (1;6) (2;5) (3;4)(3;4) (2;5) (1;6) \)
for k in range(0,m):
n=0
while n<len(seg[k])-1:
while n<len(seg[k])-1 and seg[k][n]==seg[k][n+1]:
del(seg[k][n])
n+=1 Les listes deviennent alors :
pour \(1 : (0;0) (1;1) (2;2) (3;3) (4;4) (5;5) (6;6)\)
pour \(2 : (0;0) (1;2) (2;4) (3;6) (1;4) (3;5) (5;6)\)
pour \(3 : (0;0) (1;3) (2;6) (2;3) (4;5) (1;5) (4;6)\)
pour \(4 : (0;0) (1;4) (1;2) (3;5) (2;4) (5;6) (3;6)\)
pour \(5 : (0;0) (1;5) (2;3) (1;3) (4;6) (4;5) (2;6)\)
pour \(6 : (0;0) (1;6) (2;5) (3;4)\)
nbredoublons=0
print(m,':',end=' ')
for k in range(0,m-1):
for j in range(k+1,m):
if seg[k]==seg[j]:
nbredoublons+=1
print(k,'=',j,end='; ')
print('BILAN : ',m-nbredoublons,"motifs différents") En mettant bout à bout les \(4\) morceaux de code ci-dessus, vous avez un programme fonctionnel (écrit en Python 3.8, et qui ne nécessite pas de librairie particulière).
L’analyse des résultats n’a montré aucune exception à la réciproque conjecturée. Je ne veux pas en déduire qu’elle est vraie, mais c’est encourageant.
5. Observations complémentaires
Le programme donne la liste suivante :
Il y a donc des modulos pour lesquels toutes les tables donnent des graphiques différents.
Ici, c’est le cas de \(3\;,4\;,6\;,8,\;12\) et \(24\).
En allant chercher jusqu’à \(1\;000\; 000\), et contre toute attente, je n’en ai trouvé aucun autre.
On notera qu’il s’agit des diviseurs de \(24\). Et qu’on pourrait ajouter le cas \(m=2\) (qui fournit les tables du \(0\) et du \(1\), distinctes) ainsi que, par convention le cas \(m=1\) qui ne fournirait qu’une table par définition… La condition est que les seuls inversibles modulos \(m\) soient leur propre inverse.
Sur l’OEIS, j’ai soumis la liste des nombres de motifs différents selon \(m\), à savoir :
\(1\;;2\;;3\;;4\;;4\;;6\;;5\;;8\;;7\;;9\;;7\;;12\;;8\;;12\;;13\;;14\;;10\;;16\;;11;\) etc. que le programme donne directement. Cette liste n’était en effet pas encore publiée. Étonnant pour un sujet aussi capital pour l’avenir de l’humanité.
Cela signifierait que : \(ab≡1[m]\) et \(ac≡1[m]\) qui impliquerait \(abc≡b [m]\) d’où \(c≡b[m]\), ce qui est absurde.
L’observation est donc confirmée. Il n’existe donc pas de « triplon ».
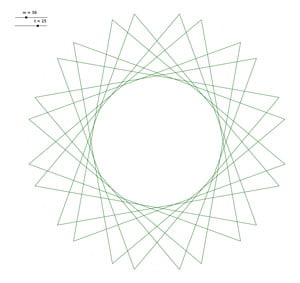
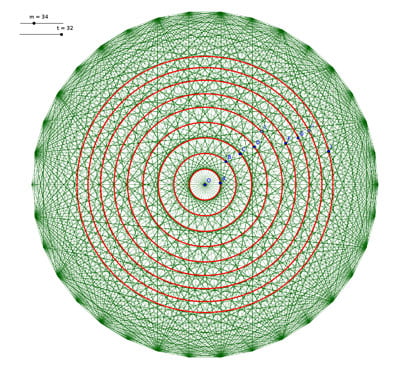
Enfin, si l’on active la trace de la séquence dans GeoGebra, en ne faisant varier que \(t\) on constate l’apparition de « cercles » concentriques qui semblent « réguliers ».
Ils ne le sont pas tout à fait. C’est une activité que l’on peut entamer avec des élèves, dans le but d’infirmer des conjectures.
Observons par exemple la figure suivante, obtenue de cette manière.
Des cercles apparaissent très clairement et leurs rayons semblent en progression arithmétique.
« Un cercle est une droite arrondie avec un trou au milieu »
Et j’ai répertorié les rayons dans LibreOffice Calc. Cela a donné les résultats ci-contre. Ce n’est qu’une apparence de progression arithmétique. En fait les rayons semblent augmenter de moins en moins avec la distance à l’origine. J’ai alors fait l’hypothèse que l’un des graphiques, pour \(t=m−1\) pouvait me fournir ces rayons.
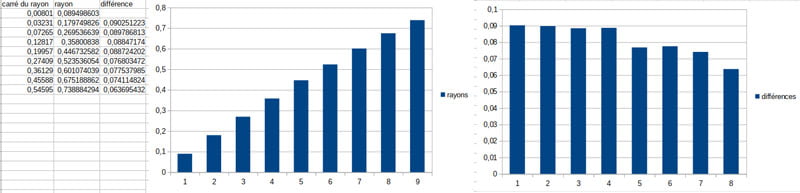
Et il s’avère en effet que tous les cercles tracés sont tangents à ces segments, puisque les cercles ne sont en fait que l’enveloppe des segments. Une illusion d’optique en d’autres termes. Tout comme les cardioïdes, néphroïdes et autres trochoïdes d’ailleurs, générées par les mêmes tables de multiplication !
Or les abscisses de ces segments sont très simples à connaître. Il s’agit de la partie réelle des exponentielles complexes qui les définissent, soit :
\(x_{k}=\cos(2k\pi\frac{m-1}{m})\) permettant au passage de déterminer le nombre de cercles qui vont apparaître soit \(\frac{m-1}{2}\) si \(m\) est impair et \(\frac{m-2}{2}\) si \(m\) est pair.
5. Perspectives pédagogiques
C’est, en outre, un prolongement de l’arithmétique modulaire pratiquée avec la pendule, et un avant-goût de celle qui les attend quelques années plus tard. Je ne peux donc qu’encourager à tenter l’expérience, et vous laisse avec quelques pépites délicieuses.
Sébastien Dumortier.
Collège Théodore Despeyrous
Beaumont de Lomagne.
- Lien vers la source Python (Sébastien Dumortier)
- Lien vers la source C++ (Sacha Bellier)
