
A partir d’un problème, cette rubrique “problème – aventure” a pour but, à travers les discussions qu’il suscite et les expérimentations réalisées, de permettre son usage dans un large spectre de classes, d’évoquer le fait de chercher, d’autres questions, connexes, satellites en quelque sorte ; un problème étant rarement isolé.
Animation et modération par Jean Aymes
Problème - Aventure n°4 - Deux énoncés (2023-2024)
Peut-on trouver quatre points alignés de sorte que leurs distances mutuelles prennent les valeurs 1, 2, 3, 4, 5 et 6 ?
Ribambelle de triangles
Dans un angle \(\widehat{XOY}\), on veut insérer des triangles isocèles successifs \(AOB\) (base \(OB\)), \(BAC\) (base \(AC\)), \(CBD\) (base \(BD\)) …
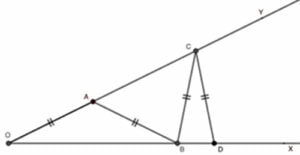
• On choisit 10° comme mesure de l’angle \(\widehat{XOY}\), est-il vrai qu’on peut insérer exactement \(8\) triangles isocèles ?
• On admet qu’on peut « revenir » vers le sommet \(O\) de l’angle, est-ce encore le cas lorsque l’angle mesure \(20°\) ?
• Combien de triangles peut-on insérer avec un angle de \(27°\) ?
• Se peut-il qu’il n’y ait aucun triangle isocèle possible ? Si oui pour quels angles ?
• L’angle peut-il être choisi de sorte qu’il y ait exactement un triangle inséré ? Exactement \(2\) triangles insérés ?
Exactement \(5\) triangles insérés ? Exactement \(10\) triangles insérés ?
Problème - Aventure n°3 - Deux énoncés (2022-2023)
L’esperluette
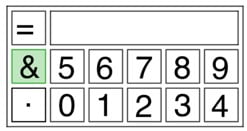
Avec dix touches pour les chiffres, une pour le point décimal, une touche opératoire \(\&\) (esperluette), une touche pour l’effectuation du calcul et un écran d’affichage, on obtient une calculatrice très simple. Peut-être la plus simple possible.
Cela semble peu réaliste !
Et si l’opération esperluette, agissant sur des nombres non nuls \(a\) et \(b\), est telle que :
Les caméléons
Dans un archipel étrange les caméléons sont gris, bruns ou rouges. Quand deux caméléons de couleurs différentes se rencontrent ils prennent tous les deux la troisième couleur.
- Sur une première île, il y a trois caméléons gris, six bruns et quatre rouges.
- Sur une deuxième île, il y a deux caméléons gris, cinq bruns et six rouges.
- Sur une troisième, il y a treize caméléons gris, quinze bruns et dix-sept rouges.
Un zoologiste s’interroge : « Pour chacune de ces îles, des circonstances de rencontres peuvent-elles produire une population de caméléons tous de la même couleur ? »
Problème - Aventure n°1 (2020-2021)
Est-il possible de choisir les signes \(\small+\) ou \(-\) devant chacun des termes de façon à avoir l’égalité :