par Yves Farcy
Tout le monde connaît cet énoncé : le robot Tom doit emprunter un pont sans garde-corps de \(n\) pas de long et de 2 pas de large. Sa démarche est très particulière :
- Soit il avance d’un pas tout droit ;
- Soit il se déplace en diagonale vers la gauche (déplacement équivalent à un pas vers la gauche et un pas tout droit) ;
- Soit il se déplace en diagonale vers la droite (déplacement équivalent à un pas vers la droite et un pas tout droit).
On suppose que ces trois types de déplacement sont aléatoires et équiprobables.
Il est tiré du sujet de bac S, Antilles – Guyane, de septembre 2013.
On cherche, à différents niveaux d’études, les expressions explicites des suites \( a_n, b_n\) et \( c_n\) représentant les probabilités du robot de se trouver aux trois positions possibles sur le pont après \(n\) déplacements puis d’obtenir la probabilité \( d_n\) d’avoir le robot sur le pont après \( n\) déplacements.
On propose également un programme Scratch présentant une simulation de ce problème.
A propos des marches aléatoires, on peut citer le bel ouvrage édité par l’école Polytechnique : Arbres et marches aléatoires et notamment le texte de d’Igor Kortchemki sur les processus Bienaymé-Galton-Watson, imaginés, au milieu du XIXème siècle, pour estimer la probabilité d’extinction des noms de familles nobles.
Les notations
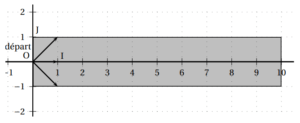
On reprend les notations de l’énoncé original. On schématise le pont par un rectangle dans le plan muni d’un repère orthonormé \((O, I, J)\) comme l’indique la figure ci-contre. On suppose que Tom se trouve au point de coordonnées \((0;0)\) au début de la traversée. On note \((x;y)\) les coordonnées de la position de Tom après \(n\) déplacements.
La définition des suites par récurrence
Pour tout entier naturel \(n\), on note :
- \(A_n\) l’évènement « après \(n\) déplacement(s), Tom se trouve sur un point d’ordonnée \(-1\) ».
- \(B_n\) l’évènement « après \(n\) déplacement(s), Tom se trouve sur un point d’ordonnée \(0\) ».
- \(C_n\) l’évènement « après \(n\) déplacement(s), Tom se trouve sur un point d’ordonnée \(1\) ».
- \(D_n\) l’évènement « après \(n\) déplacement(s), Tom se trouve sur le pont ».
- \(P_n\) l’évènement « après \(n\) déplacement(s), Tom fait « plouf » ».
On note \( a_n, b_n, c_n, d_n\) et \( p_n\) les probabilités respectives des évènements \( A_n, B_n, C_n, D_n\) et \( P_n\).
On a donc : \( a_0 =0, b_0=1\) et \( c_0=0\).
De plus la construction d’un arbre pondéré comme le suggèrait l’énoncé aide à établir :
\( a_{n+1} =\frac{a_n+b_n}{3}=c_{n+1} \)
\( b_{n+1}=\frac{a_n+b_n+c_n}{3}=\frac{2a_n+b_n}{3} \)
Enfin \( d_n=a_n+b_n+c_n=2a_n+b_n\) et \(p_n=1-d_n\).
Les propositions de solutions
On peut aborder cette méthode au lycée après l’étude des suites géométriques. Il faudra bien sûr guider la démarche ou donner les définitions par récurrence des suites \(w_n\) et \(w’_n\).
On cherche les suites \(w_n \) combinaisons linéaires de \(a_n \) et de \(b_n \) qui sont géométriques. Sans perte de généralité, on cherche donc les nombres \(k\) tels que \(w_n=ka_n+b_n \) soit géométrique. Soit \(q\) la raison de cette suite.
\(w_{n+1}=ka_{n+1}+b_{n+1} \). En remplaçant par les valeurs de \(a_{n+1}\) et \(b_{n+1}\) en fonction de \(a_{n}\) et \(b_{n}\), il vient :
\(w_{n+1}=k\frac{a_{n}+b_{n}}{3}+\frac{2a_{n}+b_{n}}{3} \) soit \(w_{n+1}=\frac{k+2}{3}a_{n}+\frac{k+1}{3}b_{n} \)
Comme \(w_n\) est géométrique de raison \(q\), \(w_{n+1}=qka_{n}+qb_{n} \) on obtient donc :
\(\frac{k+2}{3}a_{n}+\frac{k+1}{3}b_{n}=qka_{n}+qb_{n} \) et ceci pour tout \(n\).
On en déduit que \(q\) est solution du système :\(\left\{\begin{array}{ccc}q=\frac{k+1}{3}\\kq=\frac{k+2}{3}\end{array}\right. \Leftrightarrow\left\{\begin{array}{ccc}q=\frac{k+1}{3}\\k(\frac{k+1}{3})=\frac{k+2}{3}\end{array}\right.\Leftrightarrow\left\{\begin{array}{ccc}q=\frac{k+1}{3}\\k^{2}=2\end{array}\right.\)
donc \(k=\sqrt{2}\) et \(q=\frac{1+\sqrt{2}}{3}\) ou \(k=-\sqrt{2}\) et \(q=\frac{1-\sqrt{2}}{3}\).
On a donc deux suites géométriques : \(\left\{\begin{array}{ccc}w_n =\sqrt{2}a_n+b_n\\w’_n =-\sqrt{2}a_n+b_n\end{array}\right. (1)\)
Et comme \(w_0 =w’_0=b_0=1\) : \(\left\{\begin{array}{ccc}w_n =\left(\frac{1+\sqrt{2}}{3}\right)^{n}\\w’_n =\left(\frac{1-\sqrt{2}}{3}\right)^{n}\end{array}\right. (2)\)
De \((1)\) on déduit : \(\left\{\begin{array}{ccc}a_n =\frac{1}{2\sqrt{2}}(w_n-w_n’)\\b_n =\frac{1}{2}(w_n+w_n’)\end{array}\right.\) et en remplaçant par les valeurs de \((2)\)
\(\left\{\begin{array}{ccc}a_n =c_n=\frac{1}{2\sqrt{2}}\Big[\left(\frac{1+\sqrt{2}}{3}\right)^{n}-\left(\frac{1-\sqrt{2}}{3}\right)^{n}\Big]\\b_n =\frac{1}{2}\Big[\left(\frac{1+\sqrt{2}}{3}\right)^{n}+\left(\frac{1-\sqrt{2}}{3}\right)^{n}\Big]\end{array}\right.\)
Comme \(d_n=2a_n+b_n\) après calculs il vient \(d_n =\frac{3}{2}\Big[\left(\frac{1+\sqrt{2}}{3}\right)^{n+1}-\left(\frac{1-\sqrt{2}}{3}\right)^{n+1}\Big]\)
Enfin \(p_n =1-\frac{3}{2}\Big[\left(\frac{1+\sqrt{2}}{3}\right)^{n+1}-\left(\frac{1-\sqrt{2}}{3}\right)^{n+1}\Big]\)
On essaie ici d’obtenir une solution présentable en Terminale mathématiques expertes. L’intérêt est de manipuler un peu de matrice mais on se retrouve finalement sur les mêmes problématiques sur les suites que dans la proposition 1.
On peut traduire ces relations de récurrence de façon matricielle :
\(\begin{pmatrix}
a_{n+1} \\
b_{n+1}
\end{pmatrix}=\frac{1}{3}A\begin{pmatrix}
a_{n} \\
b_{n}
\end{pmatrix}\) avec \(A =\begin{pmatrix}
1& 1\\
2& 1
\end{pmatrix}\).
On aura donc :
\(\begin{pmatrix}
a_{n} \\
b_{n}
\end{pmatrix}=(\frac{1}{3})^{n}A^{n}\begin{pmatrix}
a_{0} \\
b_{0}
\end{pmatrix}\) soit \(\begin{pmatrix}
a_{n} \\
b_{n}
\end{pmatrix}=(\frac{1}{3})^{n}A^{n}\begin{pmatrix}
0 \\
1
\end{pmatrix}\)
Pour calculer \(A^{n}\) commençons par calculer \(A^{2}\).
\(A^{2}=\begin{pmatrix}
3& 2\\
4& 3
\end{pmatrix}=2A+I_{2}\). Bien sûr on peut en déduire que \(P(X) = X^{2}-2X-1\) est le polynôme minimal de \(A\) (voir troisième proposition de solution) mais ici on reste au niveau lycée.
Une récurrence immédiate, permet d’établir que \(A^{n}=\alpha_nA+\beta_nI_{2}\) avec \(\alpha_1=1\) et \(\beta_1=0\)
A cette occasion on trouve que \(A^{n+1}=A(\alpha_nA+\beta_nI_{2})\Leftrightarrow A^{n+1}=\alpha_nA^{2}+\beta_nA\Leftrightarrow A^{n+1}=(2\alpha_n+\beta_n)A+\alpha_nI\)
On a donc :\(\left\{\begin{array}{ccc}\alpha_{n+1}=2\alpha_{n}+\beta_{n}\\\beta_{n+1}=\alpha_{n}\end{array}\right.\)
Reste à expliciter \(\alpha_{n}\) et \(\beta_{n}\). On se retrouve dans la même situation que dans la première proposition de solution. On cherche les suites \(w_{n}\) combinaisons linéaires de \(\alpha_{n}\) et \(\beta_{n}\) qui sont géométriques.
On cherche donc les nombres \(k\) tels que \(w_n=k\alpha_n+\beta_n \) soit géométrique de raison \(q\).
On trouve alors que \(q=k \in \{1-\sqrt{2} ; 1+\sqrt{2}\}\) et donc deux suites :
\(w_n=(1-\sqrt{2}) \alpha_n+\beta_n= (1-\sqrt{2})^{n}\) et \(w’_n=(1+\sqrt{2}) \alpha_n+\beta_n= (1+\sqrt{2})^{n}\).
On en déduit que
\(\left\{\begin{array}{ccc}\alpha_n=\frac{1}{2\sqrt{2}}\Big[\left(1+\sqrt{2}\right)^{n}-\left(1-\sqrt{2}\right)^{n}\Big]\\\beta_n =\frac{1}{2\sqrt{2}}\Big[\left(1+\sqrt{2}\right)\left(1-\sqrt{2}\right)^{n}-\left(1-\sqrt{2}\right)\left(1+\sqrt{2}\right)^{n}\Big]\end{array}\right.\)
En reprenant \(A^{n}=\alpha_nA+\beta_nI_{2}\) et \(\begin{pmatrix}
a_{n} \\
b_{n}
\end{pmatrix}=(\frac{1}{3})^{n}A^{n}\begin{pmatrix}
0 \\
1
\end{pmatrix}\) on déduit que :
\(A^{n}=\begin{pmatrix}
\alpha_n+\beta_n&\alpha_n\\
2\alpha_n& \alpha_n+\beta_n
\end{pmatrix}\) et \(\begin{pmatrix}
a_{n} \\
b_{n}
\end{pmatrix}=(\frac{1}{3})^{n}\begin{pmatrix}
\alpha_n \\
\alpha_n+\beta_n
\end{pmatrix}\)
On retrouve \(\left\{\begin{array}{ccc}a_n =c_n=\frac{1}{2\sqrt{2}}\Big[\left(\frac{1+\sqrt{2}}{3}\right)^{n}-\left(\frac{1-\sqrt{2}}{3}\right)^{n}\Big]\\b_n =\frac{1}{2}\Big[\left(\frac{1+\sqrt{2}}{3}\right)^{n}+\left(\frac{1-\sqrt{2}}{3}\right)^{n}\Big]\end{array}\right.\) ;
\(d_n =\frac{3}{2}\Big[\left(\frac{1+\sqrt{2}}{3}\right)^{n+1}-\left(\frac{1-\sqrt{2}}{3}\right)^{n+1}\Big]\) et \(p_n =1-\frac{3}{2}\Big[\left(\frac{1+\sqrt{2}}{3}\right)^{n+1}-\left(\frac{1-\sqrt{2}}{3}\right)^{n+1}\Big]\)
On reprend la deuxième proposition au moment où on a établit que \(A^{2}=2A+I_{2}\). On en déduit que \(P(X) = X^{2}-2X-1\) est un polynôme annulateur de \(A\) et même qu’il s’agit du polynôme minimal de \(A\) puisque \(A\) n’est pas la matrice d’une homothétie.
On note \(\lambda_1=1+\sqrt{2}\) et \(\lambda_2=1-\sqrt{2}\) les deux racines de \(P\).
On écrit maintenant la division euclidienne de \(X^{n}\) par \(P(X)\) :
\(X^{n}=P(X)Q(X)+aX+b\)
En évaluant l’égalité en \(\lambda_1\) et \(\lambda_2\) on obtient le système :
\(\left\{\begin{array}{ccc}\lambda_1^{n}=a\lambda_1+b\\\lambda_2^{n}=a\lambda_2+b\end{array}\right.\Leftrightarrow\left\{\begin{array}{ccc}a=\frac{\lambda_1^{n}-\lambda_2^{n}}{\lambda_1-\lambda_2}\\b=\frac{\lambda_1^{n}\lambda_2-\lambda_2^{n}\lambda_1}{\lambda_2-\lambda_1}\end{array}\right.\)\(\Leftrightarrow\left\{\begin{array}{ccc}a=\frac{1}{2\sqrt{2}}\Big[\left(1+\sqrt{2}\right)^{n}-\left(1-\sqrt{2}\right)^{n}\Big]\\b =\frac{1}{2\sqrt{2}}\Big[\left(1+\sqrt{2}\right)\left(1-\sqrt{2}\right)^{n}-\left(1-\sqrt{2}\right)\left(1+\sqrt{2}\right)^{n}\Big]\end{array}\right.\)
En évaluant maintenant l’égalité en \(A\) :
\(A^{n}=aA+bI_2\) soit \(A^{n}=\begin{pmatrix}
a+b& a\\
2a+b& a+b
\end{pmatrix}\) et puisque \(\begin{pmatrix}
a_{n} \\
b_{n}
\end{pmatrix}=(\frac{1}{3})^{n}A^{n}\begin{pmatrix}
0 \\
1
\end{pmatrix}\) :
\(\left\{\begin{array}{ccc}a_{n}=(\frac{1}{3})^{n}a\\b_{n}=(\frac{1}{3})^{n}(a+b)\end{array}\right.\)
On retrouve \(\left\{\begin{array}{ccc}a_n =c_n=\frac{1}{2\sqrt{2}}\Big[\left(\frac{1+\sqrt{2}}{3}\right)^{n}-\left(\frac{1-\sqrt{2}}{3}\right)^{n}\Big]\\b_n =\frac{1}{2}\Big[\left(\frac{1+\sqrt{2}}{3}\right)^{n}+\left(\frac{1-\sqrt{2}}{3}\right)^{n}\Big]\end{array}\right.\) ;
\(d_n =\frac{3}{2}\Big[\left(\frac{1+\sqrt{2}}{3}\right)^{n+1}-\left(\frac{1-\sqrt{2}}{3}\right)^{n+1}\Big]\) et \(p_n =1-\frac{3}{2}\Big[\left(\frac{1+\sqrt{2}}{3}\right)^{n+1}-\left(\frac{1-\sqrt{2}}{3}\right)^{n+1}\Big]\)
En reprenant les notations de la deuxième proposition pour calculer \(A^{n}\) diagonalisons la matrice \(A =\begin{pmatrix}
1& 1\\
2& 1
\end{pmatrix}\).
On cherche les valeurs propres de \(A\) en résolvant \(det(A-\lambda I)=0\) soit \(\begin{vmatrix}
1-\lambda & 1 \\
2&1-\lambda
\end{vmatrix}=0\)
\((1-\lambda)^{2}-2=0\Leftrightarrow9\lambda^{2}-2\lambda-2=0\) qui admet deux racines distinctes :
\(\lambda_1=1-\sqrt{2}\) et \(\lambda_2=1+\sqrt{2}\)
Donc \(A\) est diagonalisable et est semblable à la matrice \(D =\begin{pmatrix}
1-\sqrt{2}& 0\\
0& 1+\sqrt{2}
\end{pmatrix}\)
On cherche maintenant les vecteurs propres afin d’obtenir la matrice de passage \(P\) : ils sont solution de \(AX=\lambda_1X\) et \(AX=\lambda_2X\).
Pour \(\lambda_1\) :
\(\left\{\begin{array}{ccc}\sqrt{2}x+y=0\\2x+\sqrt{2}y=0\end{array}\right.\Leftrightarrow y = -\sqrt{2}x\) un vecteur propre associé à \(\lambda_1\) est donc \(\begin{pmatrix}
1\\
-\sqrt{2}
\end{pmatrix}\)
Pour \(\lambda_2\) :
\(\left\{\begin{array}{ccc}-\sqrt{2}x+y=0\\2x-\sqrt{2}y=0\end{array}\right.\Leftrightarrow y = \sqrt{2}x\) et un vecteur propre associé à \(\lambda_2\) est \(\begin{pmatrix}
1\\
\sqrt{2}
\end{pmatrix}\)
La matrice de passage est donc \(P=\begin{pmatrix}
1&1\\
-\sqrt{2}&\sqrt{2}
\end{pmatrix}\) et \(P^{-1}=\frac{1}{2\sqrt{2}}\begin{pmatrix}
\sqrt{2}&-1\\
\sqrt{2}&1
\end{pmatrix}\)
On a maintenant \(A=PDP^{-1}\) et \(A^{n}=PD^{n}P^{-1}\)
\(A=\frac{1}{2\sqrt{2}}\begin{pmatrix}
1&1\\
-\sqrt{2}&\sqrt{2}
\end{pmatrix}\begin{pmatrix}
1-\sqrt{2}& 0\\
0& 1+\sqrt{2}
\end{pmatrix}\begin{pmatrix}
\sqrt{2}&-1\\
\sqrt{2}&1
\end{pmatrix}\)
\(A^{n}=\frac{1}{2\sqrt{2}}\begin{pmatrix}
1&1\\
-\sqrt{2}&\sqrt{2}
\end{pmatrix}\begin{pmatrix}
(1-\sqrt{2})^{n}& 0\\
0& (1+\sqrt{2})^{n}
\end{pmatrix}\begin{pmatrix}
\sqrt{2}&-1\\
\sqrt{2}&1
\end{pmatrix}\)
\(A^{n}=\begin{pmatrix}
\frac{1}{2}\Big[(1-\sqrt{2})^{n}+(1+\sqrt{2})^{n}\Big]&\frac{1}{2\sqrt{2}}\Big[(1+\sqrt{2})^{n}-(1-\sqrt{2})^{n}\Big]\\
\frac{1}{\sqrt{2}}\Big[(1+\sqrt{2})^{n}-(1-\sqrt{2})^{n}\Big]&\frac{1}{2}\Big[(1-\sqrt{2})^{n}+(1+\sqrt{2})^{n}\Big]
\end{pmatrix}\)
Et maintenant puisque \(\begin{pmatrix}
a_{n} \\
b_{n}
\end{pmatrix}=\left(\frac{1}{3}\right)^{n}A^{n}\begin{pmatrix}
0 \\
1
\end{pmatrix}\)
On retrouve \(\left\{\begin{array}{ccc}a_n =c_n=\frac{1}{2\sqrt{2}}\Big[\left(\frac{1+\sqrt{2}}{3}\right)^{n}-\left(\frac{1-\sqrt{2}}{3}\right)^{n}\Big]\\b_n =\frac{1}{2}\Big[\left(\frac{1+\sqrt{2}}{3}\right)^{n}+\left(\frac{1-\sqrt{2}}{3}\right)^{n}\Big]\end{array}\right.\).
\(d_n =\frac{3}{2}\Big[\left(\frac{1+\sqrt{2}}{3}\right)^{n+1}-\left(\frac{1-\sqrt{2}}{3}\right)^{n+1}\Big]\) et \(p_n =1-\frac{3}{2}\Big[\left(\frac{1+\sqrt{2}}{3}\right)^{n+1}-\left(\frac{1-\sqrt{2}}{3}\right)^{n+1}\Big]\)
C’est la version « savante » de la première proposition. On reprend les définitions par récurrence des deux suites \((a_n)\) et \((b_n)\) :
\( a_{n+1} =\frac{1}{3}(a_n+b_n) \) et donc \(b_{n}=3a_{n+1}-a_{n}\)
\( b_{n+1}=\frac{1}{3}(2a_n+b_n) \) et donc \(2a_{n}=3b_{n+1}-b_n \)
On calcule \(a_{n+2}\) et \(b_{n+2}\) :
\( a_{n+2} =\frac{1}{3}(a_{n+1}+b_{n+1}) =\frac{1}{3}(a_{n+1}+\frac{1}{3}(2a_n+b_n))=\frac{1}{3}(a_{n+1}+\frac{1}{3}(2a_n+3a_{n+1}-a{n}))=\frac{2}{3}a_{n+1}+\frac{1}{9}a_n\)
\( b_{n+2}=\frac{1}{3}(2a_{n+1}+b_{n+1})=\frac{1}{3}(\frac{1}{3}(2a_n+2b_n) +b_{n+1}) =\frac{1}{3}(\frac{1}{3}(3b_{n+1}-b_n+2b_n) +b_{n+1})=\frac{2}{3}b_{n+1}+\frac{1}{9}b_n\)
On a donc deux suites récurrentes linéaires d’ordre 2 identiques :
\( a_{n+2} =\frac{2}{3}a_{n+1}+\frac{1}{9}a_n\) et \( b_{n+2} =\frac{2}{3}b_{n+1}+\frac{1}{9}b_n\)
Seules les conditions initiales sont différentes : \(a_0=0\) et \(a_1=\frac{1}{3}\) tandis que \(b_0=1\) et \(b_1=\frac{1}{3}\).
On sait que l’espace des suites solutions est un espace vectoriel de dimension 2 dont on cherche une famille libre parmi les suites géométriques. Cela revient à résoudre l’équation caractéristique :
\(r^{2}-\frac{2}{3}r-\frac{1}{9}=0\) qui a deux racines distinctes \(r_1=\frac{1-\sqrt{2}}{3}\) et \(r_2=\frac{1+\sqrt{2}}{3}\).
On a donc :
\(a_n=\lambda\left(\frac{1-\sqrt{2}}{3}\right)^{n}+\mu\left(\frac{1+\sqrt{2}}{3}\right)^{n}\) et \(b_n=\lambda’\left(\frac{1-\sqrt{2}}{3}\right)^{n}+\mu’\left(\frac{1+\sqrt{2}}{3}\right)^{n}\)
Les conditions initiales donnent pour \(a_{n}\) :
\(\left\{\begin{array}{ccc}\lambda+\mu=0\\(1-\sqrt{2})\lambda+(1+\sqrt{2})\mu=1\end{array}\right.\Leftrightarrow\left\{\begin{array}{ccc}\lambda=-\frac{1}{2\sqrt{2}}\\\mu=\frac{1}{2\sqrt{2}}\end{array}\right. \)
On retrouve \(a_n =c_n=\frac{1}{2\sqrt{2}}\Big[\left(\frac{1+\sqrt{2}}{3}\right)^{n}-\left(\frac{1-\sqrt{2}}{3}\right)^{n}\Big]\) ;
Les conditions initiales donnent pour \(b_{n}\) :
\(\left\{\begin{array}{ccc}\lambda’+\mu’=1\\(1-\sqrt{2})\lambda’+(1+\sqrt{2})\mu’=1\end{array}\right.\Leftrightarrow\left\{\begin{array}{ccc}\lambda’=\frac{1}{2}\\\mu’=\frac{1}{2}\end{array}\right. \)
et on retrouve \(b_n=\frac{1}{2}\Big[\left(\frac{1+\sqrt{2}}{3}\right)^{n}+\left(\frac{1-\sqrt{2}}{3}\right)^{n}\Big]\) ;
et bien sûr :
\(d_n =\frac{3}{2}\Big[\left(\frac{1+\sqrt{2}}{3}\right)^{n+1}-\left(\frac{1-\sqrt{2}}{3}\right)^{n+1}\Big]\) et \(p_n =1-\frac{3}{2}\Big[\left(\frac{1+\sqrt{2}}{3}\right)^{n+1}-\left(\frac{1-\sqrt{2}}{3}\right)^{n+1}\Big]\)
Vous trouverez donc ci-joint un fichier programmé avec Scratch 2.0 sur la traversée du pont pour \(n=9\). Il peut servir de simulation de la marche aléatoire et permet de travailler par exemple les intervalles de fluctuations.
