Ce puzzle a été présenté lors d’un atelier aux journées de Grenoble, en 1995.
Le pavage présenté se trouve dans le fascicule « Objets mathématiques » de l’APMEP de Lorraine.
Le puzzle de Sam Loyd , constitué de cinq pièces est présenté ci-dessous sous la forme d’un quadrilatère.
On trouvera en fin d’article un fichier .svg de 12 puzzles pour la découpe laser.
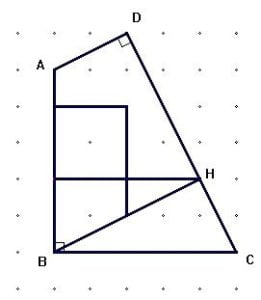
- il possède deux côtés consécutifs égaux
- deux de ses angles opposés sont droits
- les deux côtés qui ne sont pas égaux sont dans le rapport 3.
- tracé à la règle et au compas
- construction sur quadrillage
- distribution des pièces du puzzle puis reconstruction du quadrilatère de base.
Différentes exploitations, et à plusieurs niveaux sont possibles :
- on peut se contenter des figures à reconstituer, rester sous la forme du jeu du puzzle : fabriquer un carré, un rectangle, une croix grecque, un rectangle et un T

- on peut aller plus loin dans les justifications et utilisations de transformations identifiées pour passer d’une figure à l’autre (voir la présentation ci-dessous).
C’est aussi l’occasion de faire réaliser aux élèves un pavage du plan, ou bien être un point de départ vers d’autres types de pavage…(voir la présentation ci-dessous).
L’intérêt de la construction sur quadrillage est la possibilité offerte à la justification :
- dans une première phase d’analyse, pour :
– les angles droits en D et en H par étude d’angles complémentaires
– CD = 3 AD - dans un deuxième temps pour une éventuelle fabrication sur papier cartonné quadrillé
- pour caractériser les transformations utilisées :
- le calcul des angles de rotation
- détermination des vecteurs de translation…
On trouvera également ci-dessous des activités sur les angles, les périmètres et les aires dans le fichier suivant issu du site national de l’APMEP.
Enfin un fichier .svg de 12 puzzles de Sam Lloyd pour la découpe laser.
