par Yves Farcy
Le problème initial est issu de la brochure de l’Irem de Poitiers : Enseigner les mathématiques en sixième à partir des grandeurs: les volumes. Plus récemment, le groupe Activités de l’Irem de Rouen a reprit ce problème dans le cadre d’un dispositif innovant inspiré des Lesson Studies. On peut retrouver la synthèse de leur travaux autour de ce problème sur cette page. Pour ceux qui s’intéressent aux lessons studies, Blandine Masselin a publié récemment un ouvrage relatant et analysant ces expériences.
Pour le plaisir de chercher et de faire (un peu) de mathématiques, le problème a été ici complété.
On possède quatre cornières d’un mètre de long chacune avec laquelle je peux construire l’armature une caisse en bois parallélépipédique. Quelles sont les dimensions de la caisse de volume maximal ?
On cherche ici une résolution experte du problème.
Après une brève analyse, on conclut, dans un premier temps, que l’on doit découper de la même manière les quatre cornières en trois morceaux.
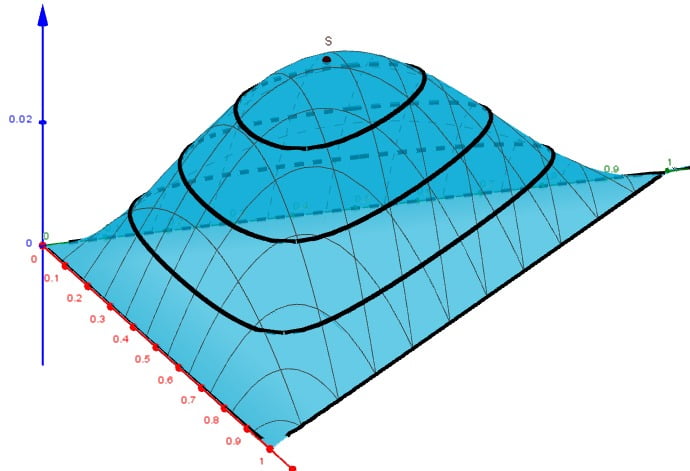
Comme \(x+y+z=1\) on a \(z=1-x-y\) avec \(0\leq x \leq 1, 0\leq y \leq 1\) et \( 0\leq z \leq 1 \) soit \(\left\{\begin{array}{ccc}0\leq x \leq 1\\0\leq y \leq 1\\0\leq x+y \leq 1\end{array}\right.\).
Le volume \(V(x,y)=xy(1-x-y)\) est une fonction de deux variables
De plus \(V\) est positive et est nulle sur les bords du triangle \(T\) i.e \(\forall(x,y)\in\mathbb{R}^2 ; V(x,0)=V(0,y)=V(x,1-x)=0\).
\(0\) est donc le minimum de \(V\) sur \(T\)
\(\left\{\begin{array}{ccc}1-2x-y=0\\1-x-2y=0\end{array}\right. \Leftrightarrow\left\{\begin{array}{ccc}x=\frac{1}{3}\\y=\frac{1}{3}\end{array}\right.\).