F. Desnoyer
fdesnoyer.maths@gmail.com
Résumé
Un petit article autour du problème du mot appliqué aux tresses en forme d’hommage à Patrick Dehornoy (1952- 2019). On y propose aussi des algorithmes programmés en Python.
1. Hommage
Patrick Dehornoy était un mathématicien français dont j’ai découvert les travaux dans une vidéo sur internet dans laquelle il essayait de montrer l’apport de l’infini aux mathématiques. À cette occasion, j’ai pu goûter aux plaisirs de la théorie des ensembles et c’est en lisant ses livres que j’ai eu le plaisir d’échanger avec lui et de découvrir sa gentillesse. Cet article est un très modeste hommage au plaisir qu’il savait communiquer à l’aide des mathématiques, en particulier les tresses dont il était un éminent spécialiste. Dans son livre [De19], qui restera l’un de ses ultimes écrits, il détaille plusieurs algorithmes et nous nous proposons, suivant [CR] de revenir sur celui que l’on appelle algorithme de « retournement » qui permet de répondre au souvent délicat problème du mot dans le cas des groupes de tresses. On verra avec le Théroème 2 qu’il y a une analogie à faire entre le tri le plus « classique » et cet algorithme au résultat non-trivial.
2. Algorithmes de tri : le classique "Tri à bulles"
2.1 Tri à bulles : principe
On va faire remonter les éléments les plus légers le long de la liste et celle-ci sera triée en fin d’itération.
On sait que cet algorithme naïf est efficace sauf sur une liste triée dans le sens inverse (c’est ce que l’on appelle son « pire cas »).
2.2 Tri à bulles : mise en œuvre
Tri à bulles
Tant que nontriee(L) faire :
si L(i)>L(i+1)
echange(L(i),L(i+1))
i=i+1
renvoyer L
Voici un programme en Python qui applique cet algorithme :
def bulle(L):
n=len(L)
nb_inv=1 #0
M=L
while nb_inv >0:
for i in range(n-1):
if M[i]>M[i+1]:
c=M[i]
M[i]=M[i+1]
M[i+1]=c
nb_inv=nb_inv-1
nb_inv=0
for i in range(n-1):
if M[i]>M[i+1]:
nb_inv=nb_inv+1
return M 3. Problème du mot - Théorie des Tresses
3.1 Introduction
La théorie des tresses est une théorie relativement récente puisque c’est Émile Artin qui en propose les premiers résultats en 1926, leur étude a aussi grandement bénéficié des généralisations obtenues par Garside vers 1969.
Par la suite, on ne supposera pas le lecteur familier des objets et on en proposera une approche simple. On pourra retrouver toute la rigueur nécessaire dans [De19] et une approche plus globale dans [De06].
Ici, notre propos est de revenir sur ce que l’on appelle le « problème du mot » qui a le bon goût d’être « décidable » dans les groupes de tresses.
3.2 Le problème du mot dans un groupe
Exemples :
Premier exemple : \(G=(a|a^n)\) ce qui signifie que l’on se donne un objet \(a\) et la relation \(a^n=1_G\) (une relation sans signe \(=\) est à lire \(\dots=1_G\) que l’on notera \(1\) à l’avenir si aucune ambigüité ne peut en découler), on reconnaît là un groupe cyclique à \(n\) éléments dont un exemple est \(\mathbb{Z}/n\mathbb{Z}\).
Deuxième exemple : \(F=(a|~)\) ce qui signifie que l’on se donne encore un objet \(a\) mais aucune relation, c’est un groupe libre à un générateur.
Troisième exemple : \(H=(a,b|ab=ba)\) ce qui signifie que l’on se donne deux objets notés \(a\) et \(b\) et la relation implique qu’ils commutent. On pourra aussi écrire \(aba^{-1}b^{-1}\) pour la relation ce qui, dans ce cas, est bien moins explicite.
Quatrième exemple :$$S=(a_1,\dots,a_n|a_i^2=1,a_ia_j=\left\{\begin{array}{ccc}a_ja_i&\text{ si }&|i-j|>1\\a_ja_ia_j^{-1}a_i^{-1}&\text{ si }&|i-j|=1\end{array}\right.$$ Reconnaître le groupe (très classique) ici présenté peut être délicat.
Problème du mot : La présentation d’un groupe cache souvent des choses comme une relation de récurrence peut masquer une suite constante derrière de nobles oripeaux. Quand un objet (une tresse par exemple) sert à un cryptage, il serait bête que l’on obtienne un codage trivial sans même le savoir. On désigne, donc, par problème du mot la recherche d’un algorithme permettant, dans un groupe donné \(\mathbb{G}\), de décider si mot est équivalent au mot « vide » (\(= 1_{\mathbb{G}}\)).
Exemples :
Le 4e exemple ci-dessus est une présentation dite de « Coxeter » du groupe symétrique \(\mathscr{S} _n\) cf [De04].
On s’intéressera par la suite au mot \(M=s_1s_2s_1s_{-2}s_{-1}s_{-2}\), si l’on ne se donne aucune règle (groupe libre à deux générateurs \(s_1\) et \(s_2\)) on en restera là.
Difficulté : il a été démontré en 1953 qu’il s’agissait d’un problème indécidable en toute généralité par Tarski
[Ta53] et, en 1986, Collins a construit des présentations finies pour lesquelles le problème du mot est indécidable.
La théorie ne semble, donc, pas être de notre côté.
4. Le cas des tresses
4.1 Notion de Tresse
Pour une introduction très riche à ce sujet, l’article [De06] est disponible.
On choisit, ici, d’omettre le point de vue géométrique au profit d’idées plus algébriques mais on proposera, bien sûr, des visualisations par la suite. Une tresse est un mot constitué de lettres choisies dans un alphabet \(\sigma_1,\dots,\sigma_{n-1}\) (on parlera de tresse à \(n\) brins).
Exemple de tresses
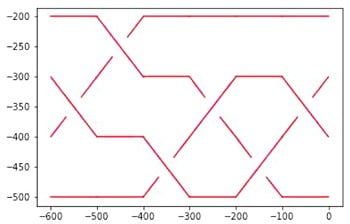
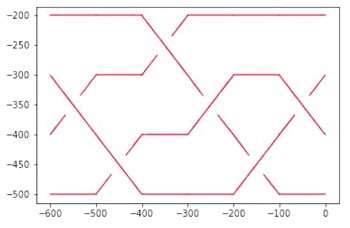
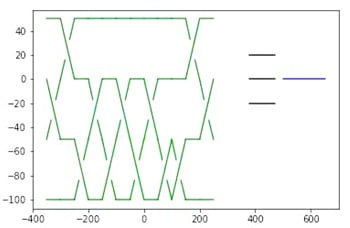
La tresse, Figure 1, est codée par le mot \(\omega=\sigma_2\sigma_3\sigma_1\sigma_2^{-1}\sigma_1^{-1}\sigma_2\).
On constate qu’il n’y pas de différence avec \(\omega~’=\sigma_2\sigma_1\sigma_3\sigma_2^{-1}\sigma_1^{-1}\sigma_2\) représenté sur la Figure 2.
Il est, par contre, plus subtil de voir qu’elle est aussi identique au mot \(\omega~^{\prime\prime}\) représenté sur la Figure 3.
C’est cette difficulté
à concevoir que des tresses d’aspects distincts et de codages distincts sont un même objet que l’on appelle
problème du mot.
4.2 Remarques sur des approches naïves
Il pourrait être tentant de confondre une tresse avec une permutation des \(n\) brins qu’elle tresse, sauf que l’application, naturelle \(s :\mathcal{B}_n\longrightarrow\mathscr{S} _n\) d’un groupe de tresses dans le groupe symétrique associé est surjective mais, clairement, pas injective car \(\mathcal{B}_n\) est infini !
Toutefois, cette approche peut apporter des idées sur un autre algorithme concernant le problème du mot. Mais ce n’est pas notre objet aujourd’hui.
Deuxième souci: la longueur (le nombre de lettres) de la tresse n’est pas un invariant comme le prouve le mot \(\omega~^{\prime\prime}\) ci-dessus qui est plus long que les mots \(\omega\) et \(\omega~’\).
4.3 Algorithme de Retournement d’un mot de Tresse
Voici l’algorithme au coeur de notre synthèse :
Retournement d’un mot
Tant que nontrie(mot) faire
k = plus-petit-echange(mot)
echange(mot(k),mot(k+1))
renvoyer mot
4.4 Relations d'Artin
Il nous faut commencer par une définition :
Définition :
On dira que deux tresses \(u,v\) sont équivalentes \(u\equiv v\) si l’on peut passer de l’une à l’autre à l’aide de l’algorithme de retournement d’un mot en un nombre fini d’étapes. On notera \(u\longrightarrow^*v\) et \(u\longrightarrow v\) en une seule étape.
Voici le premier théorème fondamental :
Le groupe \(\mathcal{B}_n\) admet pour présentation \((\sigma_1,\dots,\sigma_n|\sigma_i\sigma_j=\left\{\begin{array}{ccc}\sigma_j\sigma_i&\text{ si }&|i-j|>2\\\sigma_j\sigma_i\sigma_j\sigma_i^{-1}&\text{ si }&|i-j|=1\end{array}\right.\)
Regardons les mots \(\omega,\omega~’\)et \(\omega~^{\prime\prime}\) ci-dessus :
Si l’on « retourne » \(\omega\) on obtient \(\sigma_2\sigma_3\sigma_1^2\sigma_2^{-1}\sigma_1^{-1}\) mais si l’on retourne \(\omega~’\) on trouve encore\(\sigma_2\sigma_3\sigma_1^2\sigma_2^{-1}\sigma_1^{-1}=\omega~^{\prime\prime}\).
On a donc \(\omega\equiv\omega~’\equiv\omega~^{\prime\prime}\).
4.5 Théorème d'Ore
On appellera décomposition d’Ore d’un mot \(\omega\) la forme \(N(\omega)D(\omega)^{-1}\) obtenue à l’issue du retournement du mot \(\omega\) avec \(N,D\) qui sont deux mots constitués de tresses positives qui sont UNIQUES.
(Le théorème d’Ore a une portée plus générale qui sort de notre cadre, cf [De19].)
Les conditions suivantes sont équivalentes pour un mot de tresses \(\omega\) :
\((i)\,\,\,\,\omega\equiv\epsilon\)
\((ii)\,\,D(\omega)N^{-1}(\omega)\equiv\epsilon\)
4.6 Solution au problème du mot de tresses
On va appliquer la décomposition d’Ore de la façon suivante: soit un mot (comme notre premier exemple \(\omega\)), on lui applique l’algorithme de retournement et on obtient :
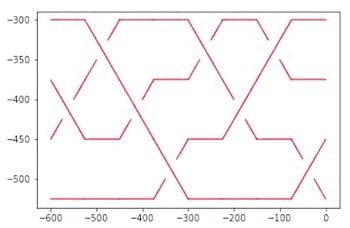
\(N(\omega)=\sigma_2\sigma_3\sigma_1^2\) et \(D(\omega)=\sigma_1\sigma_2\) c’est-à-dire que \(\omega\longrightarrow^*\sigma_2\sigma_3\sigma_1^2\sigma_2^{-1}\sigma_1^{-1}=\omega~^{\prime\prime}\) comme l’illustre la Figure 4.
On peut aussi vérifier que \(\omega\equiv\omega~^{\prime\prime}\) en appliquant la décomposition d’Ore à \(\omega\,\omega~^{\prime\prime-1}\) et l’on obtient le schéma de la Figure 5
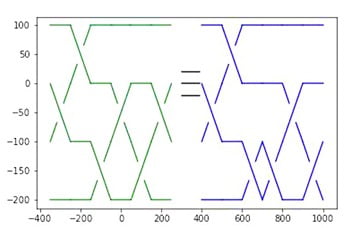
5. Illustrations à l’aide de Python
5.1 Quelques illustrations
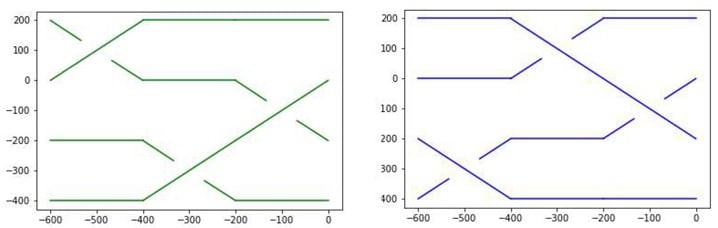
On peut vérifier que les relations de tresses sont bien validées par nos programmes en testant que les mots \(m=\sigma_1\sigma_2\sigma_1\) et \(M=\sigma_2\sigma_1\sigma_2\) sont équivalents selon les deux méthodes comme illustré sur la Figure 6
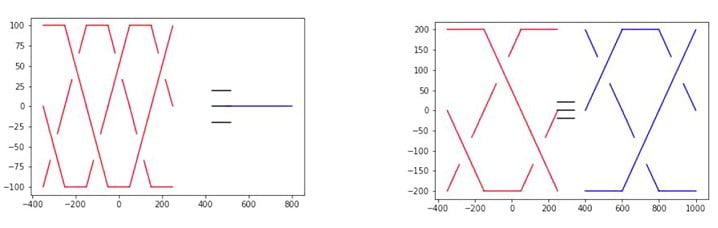
5.2 Extraits des programmes Python
Voici un petit extrait du fichier python où l’on retrouve l’algorithme de retournement ainsi que la décomposition d’Ore.
On a choisi de coder la tresse \(\sigma\) par le nombre \(i\) dans le tableau et \(\sigma^{-1}\) par \(-i\).
def max_plus (L):
n=len(L)
k=0
if L[k]>0:
while (L[k]>0 and k+1<n):
k=k+1
if k>0:
r=k-1
else :
r=0
else :
while (L[k]<0 and k+1<n):
k=k+1
if k+1<n:
r=k
else :
r=n-1
return r
def test_ech (L):
t=True
n=len(L)
if n>0:
k= max_plus (L)
while k+1<n and t:
t=(L[k+1]<0)
k=k+1
return not (t)
def echange_Artin (L,i):
a=L[i]
b=L[i+1]
t=abs(abs(a)-abs(b))
if t>1:
L[i],L[i+1]=b,a
else :
L[i]=b
L[i+1]=-a
L. insert (i+2,-b)
L. insert (i+3,a)
return L
def simplification (L):
for j in range(len(L)//2+1):
for i in range(len (L)-1):
if L[i]+L[i+1]==0:
L[i]=0
L[i+1]=0
L=[l for l in L if l!=0]
return L
def retournement (mot):
L= simplification (mot)
while test_ech (L):
k= max_plus (L)
echange_Artin (L,k-1)
L= simplification (L)
return L
def opp_mot (mot ):
return [-m for m in mot ]
def Red_Ore (mot ):
L= simplification (mot)
if test_ech (L):
L=retournement (L)
P=[]
M=[]
L=simplification (L)
if L==[]:
P=[]
M=[]
else :
k= max_plus (L)
if k>0:
for i in range(k+1):
P. append(L[i])
for j in range(1,len (L)-k):
M. append(L[k+j])
M=M[::-1]
return P, opp_mot (M)
def pb_mot_vide (mot):
M=mot
Mp ,Mm= Red_Ore (M)
L= retournement ( opp_mot (Mm)+Mp)
return L==[]
def test_equiv (T1 ,T2):
t= False
if T2==[]:
t= pb_mot_vide (T1)
else :
Test =T1+ opp_mot (T2[::-1])
t= pb_mot_vide ( Test )
return t 6. Sources
Co86 : D. Collins, A simple presentation of a group with unsolvable word problem, 1986, Illinois Journal of Mathematics
CR : J. Riou et X. Caruso, Groupes des Tresses d’Artin (mémoire de Magistère)
De08 : P. Dehornoy, Braids and Self-distributivity, 2008, Birkaüser
De09 : P. Dehornoy, Braids-based cryptography, disponible sur internet
De18 : P. Dehornoy, la Théorie des Ensembles, 2018, ed. Calvage et Mounet
De19 : P. Dehornoy, Le Calcul des Tresses, 2019, ed. Calvage et Mounet
De06 : P. Dehornoy, Le Calcul des Tresses, in Bulletin Vert n°465, 2006
Ta53 : A. Tarski, Undecidable Theories, 1953, North-Holland.
