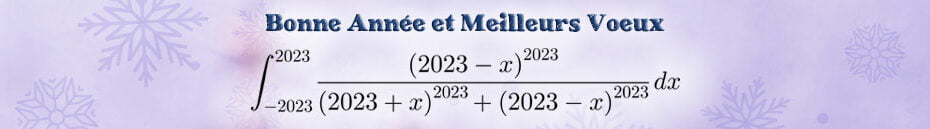La valeur de cette jolie intégrale est bien sûr \(2023\) et vous pourrez vous en reservir l’an prochain !
En effet, si l’on définit pour tout \(n\in\mathbb{N}\) $$I_{n}=\int_{-n}^{n} \frac{(n-x)^{n}}{(n+x)^{n}+(n-x)^{n}}dx$$Le changement de variable \(u=-x\) donne :$$I_{n}=\int_{-n}^{n} \frac{(n+x)^{n}}{(n+x)^{n}+(n-x)^{n}}\;dx$$On a donc $$2I_{n}=\int_{-n}^{n}\;dx$$d’où le résultat : $$I_{n}=n$$L’idée originale vient du mathématicien Srinivasa Raghava qui proposait l’intégrale : $$\int_{-2023}^{2023} \frac{\sqrt[2023]{2023-x}}{\sqrt[2023]{2023-x}+\sqrt[2023]{2023+x}}\;dx$$ qui pour les mêmes raisons que précédemment vaut \(2023\).
Il est à noter que les algorithmes des calculatrices n’ont aucun mal à calculer cette dernière contrairement à celle proposée.
On trouvera par ailleurs, sur le fil de ce mathématicien, d’autres propositions très originales !